对抗样本设计——FGSM学习记录
对抗样本设计——FGSM学习记录
什么是对抗样本
对于图像分类模型,假设我们对输入的图片进行恶意篡改,例如在原图片上叠加了一层由攻击者设计过的扰动(或噪声),会误导分类模型给出完全错误的分类结果。这种被添加了噪声的图片便是我们所说的对抗样本,这体现了分类模型对于对抗样本的脆弱性。
先看下图效果,通过对一个大熊猫照片加入一定的扰动(即噪音点),输入分类model之后就被判断为长臂猿。这种结果是很滑稽但是却很值得我们思考的,对抗样本为何会存在,我们又该如何应对。
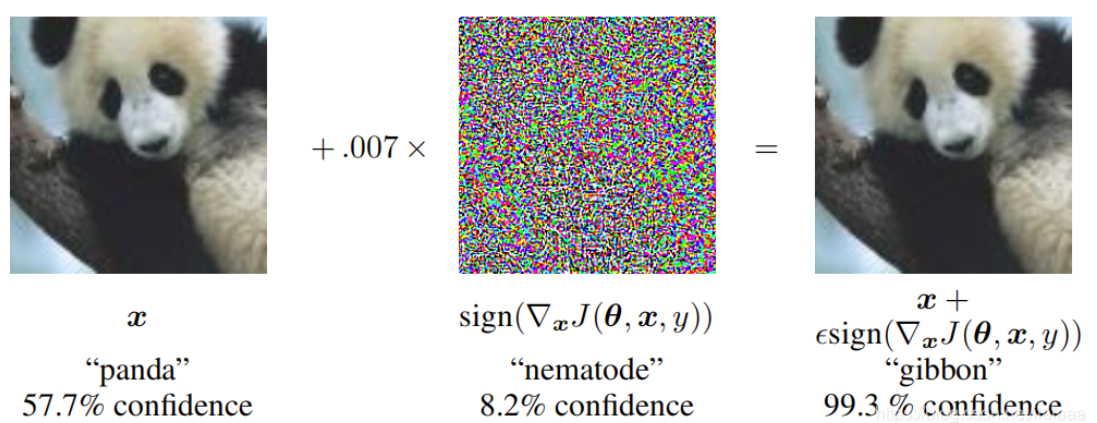
对抗样本为何存在
神经网络由多层神经元组成,每个神经元的输出是输入特征的线性组合经过非线性激活函数后的结果。这个运算过程大致要经历3步:
计算权重
\(x_1 -> w_1*x_1\)
添加偏置
\(w_1*x_1 + w_2*x_2 + b\)
计算激活函数
\(y = f(w_1*x_1 + w_2*x_2 + b)\)
此处的激活函数一般使用的是sign函数(输入为负取-1,为正取1)
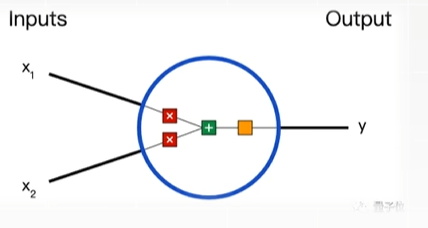
尽管非线性激活函数增加了模型的表达能力,但线性组合部分仍然保留了线性模型的敏感性。
对抗样本的生成正是利用了这一点,通过在输入数据中添加精心设计的噪声,影响神经元的线性组合结果,从而误导模型的输出。
对抗样本的线性解释
对抗样本\(\widetilde{x}\)是由原样本\(x\)上直接施加扰动\(\eta\)得到的,即\(\widetilde{x} = x + \eta\),那么考虑到权重向量\(w\)和对抗样本\(\widetilde{x}\)的点积为\(w\widetilde{x} = wx + w\eta, |\eta|<\epsilon\)
可以看出,对抗扰动使得激活函数的输入增加了\(w\eta\)
假设权重向量\(w\)有\(n\)个维度,且权重向量中元素的平均值为\(m\),那么激活函数的输入会多出\(\epsilon m n\)
因此,即使攻击者设计的扰动\(\eta\)是微小的,并不会随模型维度\(n\)的变化而变化,但是由扰动\(\eta\)导致的\(\epsilon m n\)却会随着模型维度\(n\)而线性增长
所以对抗样本的线性解释表明,对于线性模型而言,如果其输入样本有足够大的维度,那么线性模型也就容易受到对抗样本的攻击
非线性模型的线性扰动——FGSM
于是根据对抗样本的线性解释,有人提出了一种快速生成对抗样本的方法,也就是Fast Gradient Sign Method(FGSM)方法
假设模型的参数值为\(\theta\),模型的输入是\(x\),\(y\)是模型对应的label值,\(J(\theta,x,y)\)是训练神经网络的损失函数。那么对于某个特定的模型参数\(\theta\)而言,FGSM方法的损失函数将近似线性化,从而或者保证无穷范数限制的最优的扰动,公式如下:
\(\eta = \epsilon sign (\nabla_x J(\theta,x,y))\)
详细解释
模型参数和输入:
- \(\theta\) 表示模型的参数,例如神经网络中的权重和偏置。
- \(x\) 是模型的输入,例如一张图像。
- \(y\) 是输入 \(x\) 对应的真实标签。
损失函数:
- \(J(\theta,x,y)\) 是模型的损失函数,用于衡量模型输出与真实标签之间的差异。常见的损失函数包括交叉熵损失、均方误差等。
梯度计算:
- \(∇_xJ(\theta,x,y)\) 表示损失函数 J 对输入 \(x\) 的梯度。这个梯度向量的每个元素表示输入 \(x\) 的每个维度(例如图像的每个像素)对损失函数的贡献。
符号函数:
- \(sign (\nabla_x J(\theta,x,y))\)是梯度的符号函数,它将梯度向量中的每个元素转换为 +1 或 -1,具体取决于梯度的正负。这一步是为了确保扰动 η 的方向与梯度方向一致。
扰动生成:
- \(\eta = \epsilon sign (\nabla_x J(\theta,x,y))\)表示生成的扰动。这里的 ϵ 是一个超参数,控制扰动的幅度。无穷范数限制意味着每个维度的扰动绝对值不超过 ϵ。
对抗样本生成:
最终的对抗样本 \(\widetilde{x}\) 通过将扰动 η 加到原始输入 \(x\) 上得到:
\(\widetilde{x} = x + \eta =x + \epsilon sign (\nabla_x J(\theta,x,y))\)
为什么这样有效
- 线性近似:
- FGSM 方法假设在当前模型参数 \(\theta\) 下,损失函数 J 对输入 \(x\) 的关系近似为线性。这种线性近似使得我们可以使用梯度信息来快速找到最优的扰动方向。
- 无穷范数限制:
- 通过使用符号函数 sign,我们确保每个维度的扰动绝对值不超过 ϵ。这不仅符合无穷范数的定义,还使得生成的对抗样本在视觉上与原始样本非常接近。
- 最大化损失:
- 扰动 η 的方向与梯度方向一致,这意味着我们朝着使损失函数增加最快的方向添加扰动。这样可以确保生成的对抗样本能够有效地误导模型。